Co to jest logika matematyczna?
Logika matematyczna- dział matematyki, który wyodrębnił się jako samodzielna dziedzina na przełomie XIX i XX wieku wraz
z dążeniem do dogłębnego zbadania podstaw matematyki. Koncentruje się ona na analizowaniu zasad rozumowania oraz pojęć z nim związanych z wykorzystaniem sformalizowanych oraz uściślonych metod i narzędzi matematyki.
Zdanie w logice
Zdaniem w logice nazywamy każde zdanie oznajmujące, o którym możemy jednoznacznie stwierdzić czy jest prawdziwe czy fałszywe. Zdanie oznaczać będzie małymi literami p, q, r itp., prawdę zaś 1, a fałsz 0.
Przykłady
Zdanie: Wartość logiczna
~ p czytamy: ,,nieprawda, że p”
Przykłady:
Nieprawda, że mam 20 zł.
Nieprawda, że trójkąt ma 3 boki.

Koniunkcja - zdanie złożone powstałe z dwóch zdań prostych połączonych funktorem koniunkcji: ∧.
p ∧ q czytamy: ,,p i q”
Przykład:
r: Mateusz ma rower i komputer.
p: Mateusz ma rower.
q: Mateusz ma komputer.
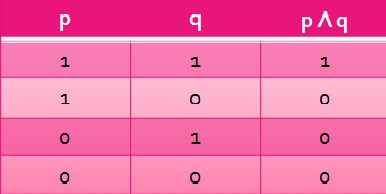
Koniunkcja jest prawdziwa tylko wtedy, gdy wszystkie zdania proste są prawdziwe.
Alternatywa
Alternatywa - zdanie złożone powstałe z dwóch zdań prostych połączonych funktorem alternatywy: V.
p V q czytamy ,,p lub q”
Przykład:
r: Jutro pójdę do znajomych albo do teatru.
p: Jutro pójdę do znajomych.
q: Jutro pójdę do teatru.

Alternatywa jest prawdziwa, gdy przynajmniej jedno zdanie proste jest prawdziwe.
Implikacja - zdanie złożone powstałe z dwóch zdań prostych połączonych funktorem implikacji: =>.
p => q czytamy: ,,z p wynika q” lub ,,jeżeli p to q”]
Przykład:
r: Jeżeli nauczę się na sprawdzian to dostanę dobrą ocenę.
p: Nauczę się na sprawdzian.
q: Dostanę dobrą ocenę.
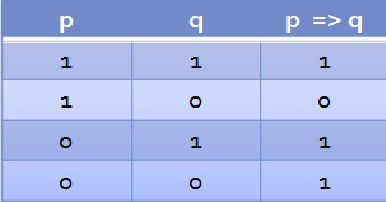
Z prawdy nie może wynikać fałsz.
W przypadku implikacji, jeśli poprzednik jest prawdziwy, to następnik nie może być fałszywy.
Równoważność zdań
Równoważność - zdanie złożone powstałe z dwóch zdań prostych połączonych funktorem równoważności ó.
pó q czytamy: ,,p wtedy i tylko wtedy, gdy q’’
Przykład:
r: „Liczba 675 jest podzielna przez 9 wtedy
i tylko wtedy, gdy suma 6, 7 i 5 jest podzielna przez 9.
p: „Liczba 675 jest podzielna przez 9”
q: „ Suma 6, 7 i 5 jest podzielna przez 9”

Równoważność jest prawdziwa tylko wtedy, gdy zdania ją tworzące mają tę samą wartość logiczną.
Prawa logiczne (tautologia)
ani przeciwnej i przeciwstawnej!
Wykażemy, że implikacje p => q oraz q => p nie są równoważne.
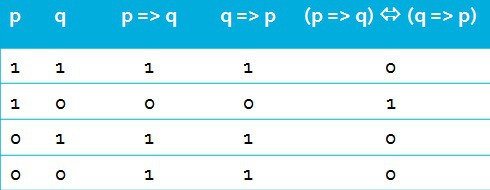
Widzimy, że w ostatniej rubryce mamy trzy 0 co świadczy o tym, że implikacje nie są równoważne.
Własność tych czterech implikacji można graficznie przedstawić w tzw. kwadracie logicznym.
Równoważne są implikacje znajdujące się na przekątnych tego kwadratu, natomiast nie są równoważne implikacje przy każdym z jego boków.

Zamiana równoważności na koniunkcję implikacji prostej i odwrotnej (p ó q) ó [(p => q) ^ (q => p)].
Z prawa tego często korzystamy.
Na przykład zamiast mówić:
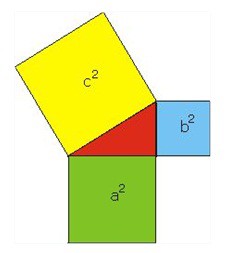
Jeżeli trójkąt ABC jest prostokątny to c2 = a2 + b2.
I Prawo De Morgana
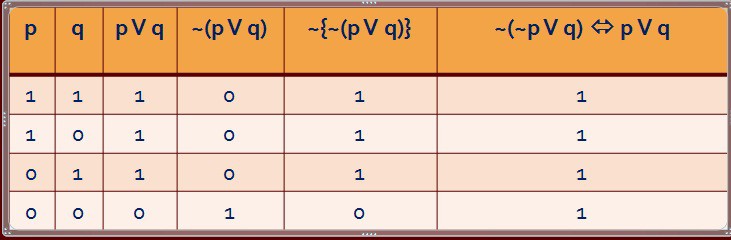
Sprawdźmy czy wyrażenie ~(p V q) ó (~p) V (~q) jest prawem logicznym.

Pokazaliśmy, że wyrażenie: ~(p V q) ó (~p) V (~q) jest prawem logicznym.
Wypowiemy je: Zaprzeczeniem alternatywy dwóch zdań jest koniunkcja zaprzeczeń tych zdań.
II Prawo De Morgana
Sprawdźmy czy wyrażenie: ~(p ^ q) ó(~p) V (~q) jest prawem logicznym.
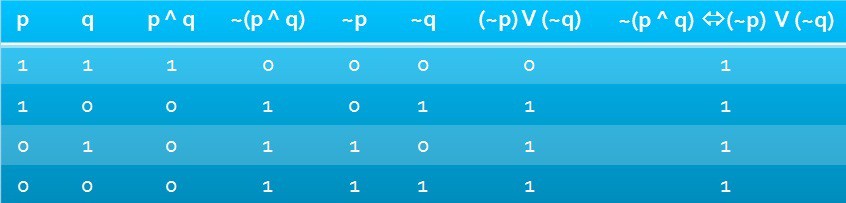
Wypowiemy je: Zaprzeczeniem koniunkcji dwóch zdań jest alternatywa zaprzeczeń tych zdań.
Tworzenie nowych praw logicznych
Nowe prawa logiczne możemy tworzyć w oparciu o te, które już znamy.
Wystarczy wykorzystać metodę podstawiania, czyli napisać dowolne wyrażenie zamiast dowolnej wybranej przez siebie literki.
Przykład:
~(~p) ó p (prawo podwójnego zaprzeczenia)
Za p możemy podstawić dowolne wyrażenie które przyjdzie nam do głowy np. p V q.
Powstaje następujące wyrażenie: ~{~(p V q)} ó p V q, które po sprawdzeniu np. metodą zerowo-jedynkową także okazuję się tautologią.