Co oznacza logarytm?
Logarytm przy podstawie a z liczby b oznacza liczbę, będącą potęgą, do której podstawa a musi być podniesiona, aby otrzymać liczbę b.
Logab= c bo ac= b a,b>0 oraz a ≠ 1
Przykłady
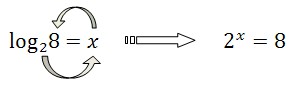
log28=3 bo 23=8
log327=3 bo 33=27
log22=1 bo 21=2
log4216=4 bo 44=216
log71=0 bo 70=1
Własności i przykłady
log41=0 bo 40=1
log22= 1 bo 21=2
log3 92= 2 log39 bo log392=22=4
2 log39=2*2=4
4log416 = 16 bo 4log416=42=16
¢Logaxk = k logax
log3 92 = 2 log39 bo log392= 22=4
2 log39 = 2*2=4
log216 / log24= log216=4
¢logab + logac = loga(b * c)
log22 + log28 = log2(2*8)=log2=16=4
¢logab - logac = loga(b / c)
log254 - log26 = log2(54/6)=log29=3
LOGARYTM DZIESIĘTNY
Logarytm dziesiętny to logarytm przy podstawie 10.
Logarytm dziesiętny liczby b oznaczamy logb.
Logarytm dziesiętny odgrywa dużą rolę w matematyce i naukach matematyczno-przyrodniczych.
Przykłady:
log0,1=-1 bo 10-1=0,1
log10=1 bo 101=10
log100=2 bo 102=100
Historia logarytmów
¢Logarytmy odkrył matematyk szkocki John Neper ok. roku 1614. Przyjaciel Nepera, Henry Briggs- matematyk angielski,
wprowadził logarytmy dziesiętne.


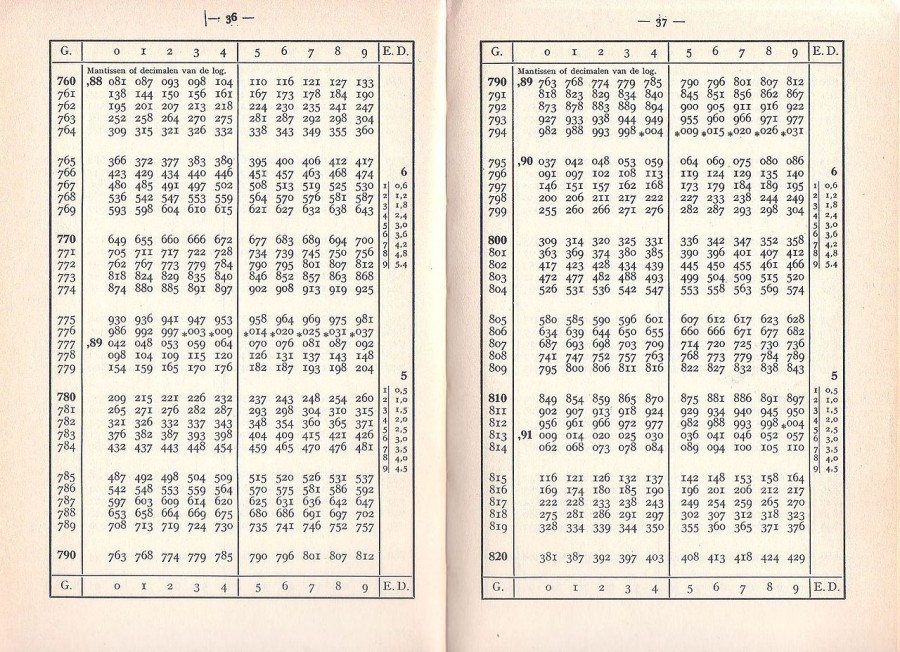
Tablica logarytmiczna
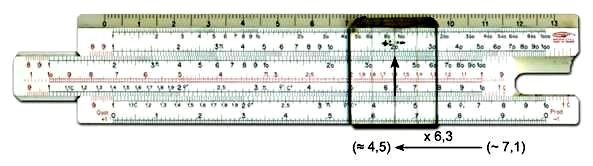
Suwak logarytmiczny
Suwak logarytmiczny (suwak rachunkowy) – prosty przyrząd ułatwiający obliczenia, powszechnie używany przez inżynierów do końca lat 80. XX wieku. Wynaleziony w 1632 roku przez Williama. Oughtreda.
Zastosowanie logarytmów dziś
Logarytmy dziesiętne znalazły zastosowanie w chemii. Odczyn roztworu to cecha związana ze stężeniem jonów wodorowych [H+] ze stężeniem jonów wodorotlenkowych [OH-].
Rodzaje odczynów roztworów:
§[H+] = [OH-] odczyn obojętny
[H+] = 10-7 mol/dm3 [OH-] = 10-7 mol/dm3
§[H+] < [OH-] odczyn zasadowy
§[H+] > [OH-] odczyn kwasowy
Chemicy posługują się „stopniami kwasowości”, zwanymi pH, które określa się wzorem: pH = -log[H+]
Dla czystej chemicznie wody mamy: pH = -log10-7=7
Wartość pH roztworów wodnych waha się w przedziale od 0 do 14.
Strony z których korzystałyśmy
¢ http://www.matemaks.pl/logarytmy.php?tid=501
Komentarze